Skip to main content

Displacer Level Measurement Calculations

 Displacer Level Measurement Calculations

Problem 1 :-

A steel displacer of volume 0.25 cubic feet is 50% immersed in oil of relative density 0.78;

the density of steel = 490 lbs per cubic foot

the density of water = 63 × lbs per cubic foot

Calculate the apparent weight of the displacer.

true weight of displacer = 0.25 × 490 = 122.5 lbs

volume of oil displaced = 0.25 × 0.5 = 0.125 cubic feet

weight of oil displaced = (0.125 × 0.78 × 63) lbs = 6.143 lbs

∴ Apparent weight of displacer = true weight − displaced weight

Apparent weight of displacer = 122.5 − 6.143 lbs = 116.36 lbs

Problem 2 :-

A steel displacer of volume 0.1 cubic feet is to be used as a level sensor in a vessel to store water.
Calculate the following;
1:- the maximum and minimum weights of the displacer.
2:- the maximum range of level able to be sensed, if the diameter of the displ. is 2 inch.
true weight of displacer = 0.1 × 490 lbs = 49 lbs

volume of water displaced = 0.1 cubic feet

weight of water displaced = 0.1 × 63 lbs = 6.3 lbs

∴ min. weight of the displacer = 49 − 6.3 lbs = 42.7 lbs

∴ max. weight of the displacer = 49 lbs

volume of the sensor = πr2L

Note : π = 3.142, 1 in = 1/12 ft = 0.0833ft

volume of the sensor ⇒ 0.1 ft3 = 3.142 × (0.0833)2 × L

0.1 ft3 = 0.0218 × L

hence, the length of displacer, L = 0.1 / 0.0218 = 4.587 ft , or 55 inches

Problem 3 :-

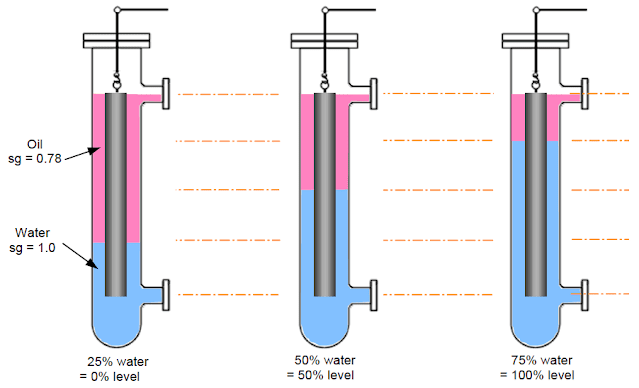
A steel displacer 1 metre long, and volume of 1000 CCs. is to be used to measure the interface level in an oil and water separator. The SG of oil is 0.78, the density of water is 1 kg/litre. Density of steel is 8000 kg per cubic meter.
Find,
1:- the diameter of the displacer.
2:- the displacer weight in air, oil & water.
3:- the “0%” and “100%” weights, if the 50% interface level is set at the displacer’s mid-point, and the span is 0.5 metres.
The displacer is assumed to be totally covered with oil or water.
volume of the sensor = πr2L

1000 c.c.s = 3.142 × r2 × 100 cm

thus, we now have, r2 =  1000 / (3.142 x 100 ) = 3.183 cm2

∴ the radius of displacer, r = Sqrt (3.183) cm = 1.78 cm

hence, the diameter of displacer = 1.78 × 2 cm = 3.56 cm

displacer’s weight in air = density × volume

Note that volume unit has to be inconsistent with density unit 1 ccs = 10−6 m3

= 8000 kgm−3 × (1×103/106) m3  = 8.0 kg

displacer’s weight in oil = (weight in air) − (weight loss in oil)

= 8.0 – (0.5 × 1 × 0.78) kg = 7.61 kg

displacer’s weight in water = (weight in air) − (weight loss in water)

= 8.0 – (0.5 × 1 × 1) kg = 7.50 kg

at 0% interface level, the displacer’s length will be covered 25% with water and 75% with oil. Hence, the displacer’s total weight will be made up of 75% of its weight in oil and 25% weight in water;

∴ displacer weight at 0% = (0.75 × 7.61) + (0.25 × 7.5) = 7.582 kg

at 50%, the displacer’s total weight will be made up of 50% weight in water, and 50% weight in oil;

∴ displacer weight at 50% = (0.5 × 7.61) + (0.5 × 7.5) = 7.555 kg

at 100%, the displacer’s total weight will be made up of 75% weight in water, and 25% weight in oil;

∴ displacer weight at 50% = (0.25 × 7.61) + (0.75 × 7.5) = 7.527 kg

Article Source : N. Asyiddin






Labels:

Comments

Post a Comment

Popular posts from this blog

PLC Program for Mixing Tank

 Create a ladder diagram for controlling a batch mixing process. Implement a PLC program for mixing tank or Mixing Process using PLC Ladder Logic. PLC Program for Mixing Tank Fig : Mixing tank A tank is used to mix two liquids. The required control circuit operates as follows: A. When the START button is pressed, solenoids A and B energize. This permits the two liquids to begin filling the tank. B. When the tank is filled, the float switch trips. This de-energizes solenoids A and B and starts the motor used to mix the liquids together. C. The motor is permitted to run for 1 minute. After 1 minute has elapsed, the motor turns off and solenoid C energizes to drain the tank. D. When the tank is empty, the float switch de- energizes solenoid C. E. A STOP button can be used to stop the process at any point. F. If the motor becomes overloaded, the action of the entire circuit will stop. G. Once the circuit has been energized, it will continue to operate until it is manually stopped. Solution...
1 comment
Read more

Ferrules and Cross Ferruling

 Ferrules are identification labels provided for every wire terminations in an instrument, equipment, or electrical/instrumentation control panels. These tube-shaped sleeves can be inserted easily on each individual wire in a multi-core cable. In earlier days fixed digits/letters are used as ferrules, but now Instrumentation engineers/technicians prints out desired ferrules by using a ferrule printing machine. Typical Ferrule The numbers/ letters on the ferrules will be given as per the approved electrical hook up or loop diagrams. This helps technicians to easily identify a particular loop/wiring from a series of terminal blocks and to troubleshoot the desired terminal connection. Separate numbers on the ferrules distinguish the positive and negative polarities of wires, thus ensure the polarity protection of the instrument. Cross Ferruling  As a wire is connected on its both ends, it is quite useful to use a cross reference method for wire identification. Unlike normal ferru...
Post a Comment
Read more

What is Relay? How it Works? Types, Applications, Testing

 We use relays for a wide range of applications such as home automation, cars and bikes (automobiles), industrial applications, DIY Projects, test and measurement equipment, and many more. But what is Relay? How a Relay Works? What are the Applications of Relays? Let us explore more about relays in this guide. What is a Relay? A Relay is a simple electromechanical switch. While we use normal switches to close or open a circuit manually, a Relay is also a switch that connects or disconnects two circuits. But instead of a manual operation, a relay uses an electrical signal to control an electromagnet, which in turn connects or disconnects another circuit. Relays can be of different types like electromechanical, solid state. Electromechanical relays are frequently used. Let us see the internal parts of this relay before knowing about it working. Although many different types of relay were present, their working is same. Every electromechanical relay consists of an consists of an Elect...
1 comment
Read more